
Vector
En física, un vector (también llamado vector euclidiano o vector geométrico) es una magnitud física definida en un sistema de referencia que se caracteriza por tener módulo (o longitud) y una dirección (u orientación).
definición de vector fijo Un vector fijo es un segmento orientado. Es decir, un par ordenado de puntos. El primero se denomina origen y el segundo extremo del vector. Cuando ambos puntos coinciden se denomina vector nulo.
Para describir un vector fijo se nombran su origen y su extremo con una flecha por encima. 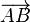
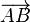

Componentes de un vector
En un sistema coordenado de dos dimensiones, cualquier vector puede separarse en el componente x y el componente y.

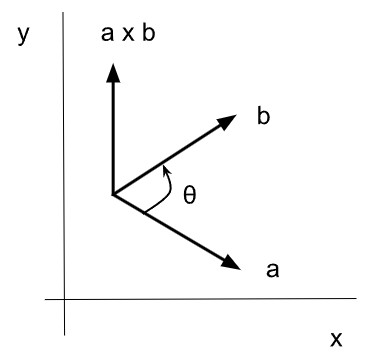
Por ejemplo, en la figura siguiente mostrada, el vector  se separa en dos componentes, vx y vy . Digamos que el ángulo entre el vector y su componente x es θ.
se separa en dos componentes, vx y vy . Digamos que el ángulo entre el vector y su componente x es θ.
 se separa en dos componentes, vx y vy . Digamos que el ángulo entre el vector y su componente x es θ.
se separa en dos componentes, vx y vy . Digamos que el ángulo entre el vector y su componente x es θ.
El vector y sus componentes forman un triángulo rectángulo como se muestra a continuación.

En la figura anterior, los componentes pueden leerse rápidamente. El vector en la forma componente es  .
.
 .
.
Las relaciones trigonométricas dan la relación entre la magnitud del vector y los componentes del vector.


vx = v cos θ
vy = v sin θ
Ejemplo:
La magnitud de un vector  es de 10 unidades y la dirección del vector es de 60° con la horizontal. Encuentre los componentes del vector.
es de 10 unidades y la dirección del vector es de 60° con la horizontal. Encuentre los componentes del vector.
 es de 10 unidades y la dirección del vector es de 60° con la horizontal. Encuentre los componentes del vector.
es de 10 unidades y la dirección del vector es de 60° con la horizontal. Encuentre los componentes del vector.
F x = F cos 60°

= 5
F y = F sin 60°


Así, el vector  es
es  .
.
 es
es  .
.Representación Gráfica
Gráficamente, un vector se representa como una flecha ubicada en un eje de coordenadas. En esta flecha podemos identificar cada uno de los elementos que lo conforman y que estudiamos en el apartado anterior, además de algunos más.
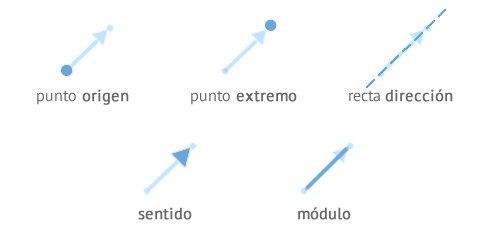
- Tienen un punto desde el que nace la flecha llamado origen o punto de aplicación.
- De igual forma, tienen otro punto donde termina la flecha llamado extremo.
- La recta sobre la que "descansan" los puntos de extremo y origen se denomina dirección o recta soporte.
- La distancia entre el punto origen y extremo corresponde con su módulo. A mayor distancia entre ellos, el módulo será mayor.
- La punta de la flecha determina su sentido, dentro de los dos posibles que se podría dibujar siguiendo su dirección, es decir hacia un lado de la recta o hacia el otro.


SUMA DE VECTORES
Con los vectores podemos realizar una serie de operaciones. Una de ellas es la suma. Podemos realizar la suma de vectores desde dos puntos de vista: matemática y gráfica.
SUMA de VECTORES MATEMÁTICA
Para realizar la suma matemática de vectores, lo único que tenemos que hacer es sumar las respectivas componentes de los vectores sumados, obteniendo así, el vector suma.
Para realizar la suma matemática de vectores, lo único que tenemos que hacer es sumar las respectivas componentes de los vectores sumados, obteniendo así, el vector suma.
Sean A y B dos vectores centrados en el origen y cuyos extremos son (ax,ay ) y (bx, by) , respectivamente . Entonces , la suma de ambos vectores esta dada por :
A+B = (ax , ay)+(bx , by) = (ax+bx , ay + by )
RESTA DE VECTORES
el vector es una magnitud que se grafica como un segmento que tiene su origen en un punto A y se orienta hacia su extremo (el punto B). El vector, por lo tanto, es un segmento AB.
EJEM
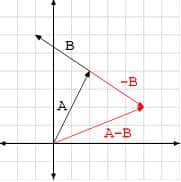
AB – DE, siendo AB (-3, 4) y DE (5, -2) de acuerdo a la posición de los vectores en el plano cartesiano. Teniendo en cuenta lo dicho sobre la suma del opuesto, deberíamos plantear la operación de este modo:
(-3, 4) – (5, -2)
(-3-5, 4+2)
(-8, 6)
(-3-5, 4+2)
(-8, 6)
MULTIPLICAION DE VECTORES
En general si OP = ( A, B ) Y K es un real cualquiera , las componentes de un vector k * OP se obtiene de la siguiente forma k* OP = k * ( a , b ) = (k*a , k*b )
Ejemplo
SI u =(-1, 3 ) y k =3 , entonces :
ku = 3* (-1,3) = (-3 , 9)
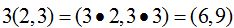
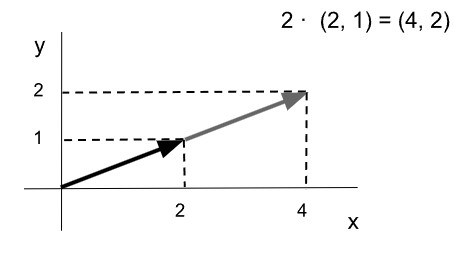
Si digo la intensidad de una fuerza es de 20 kilos,en este caso necesito conocer, la dirección, el sentido y el lugar donde aplico la fuerza. En el primer caso me refiero a magnitudes escalares, en el segundo, a magnitudes vectoriales Podemos multiplicar las coordenadas de un vector por un escalar: 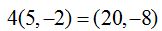
En la figura siguiente tienes el vector a que lo multiplicamos 3:
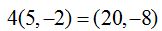
En la figura siguiente tienes el vector a que lo multiplicamos 3:
Respuesta: 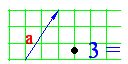

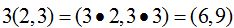
ku

No hay comentarios.:
Publicar un comentario