ÁREA Y PERÍMETRO DEL TRIANGULO

Perímetro del triángulo

Para obtener el perímetro del triángulo se suman las longitudes de sus lados.

Ejemplos

Obtener el perímetro y el área de las figuras que se mencionan en los siguientes casos.

Ver vídeo (para recordar cómo obtener el área de un triángulo).

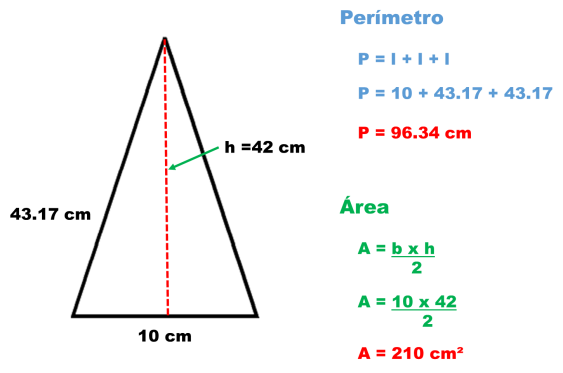
1.- Un triángulo cuya base mide 10 cm, su lado 43.17 cm y su altura 42 cm

Área del triangulo

El área de un triángulo es igual a base por altura partido por 2.La altura es la recta perpendicular trazada desde un vértice al lado opuesto (o su prolongación).

Ejemplos

Algunos ejemplos aplicando la Fórmula de Herón:

1) Si tenemos un triángulos con lados 4, 5 y 9, podemos averiguar su área utilizando la fórmula de Herón de la siguiente forma:

-Calculamos el semiperímetro:

-Entonces s = 9

-Ahora aplicamos la fórmula de Herón:

Sea un triángulo de lados conocidos, siendo estos a=4 cm, b=5 cm y c=3 cm. Calcularemos su área por la fórmula de Herón.

Primero calcularemos el semiperímetro (s).

Ejemplo de un triángulo para el cálculo de su área por la fórmula de Herón.

Cálculo del semiperímetro de un triángulo.

Ahora aplicamos la fórmula de Herón:

Cálculo del área de un triángulo por la fórmula de Herón.

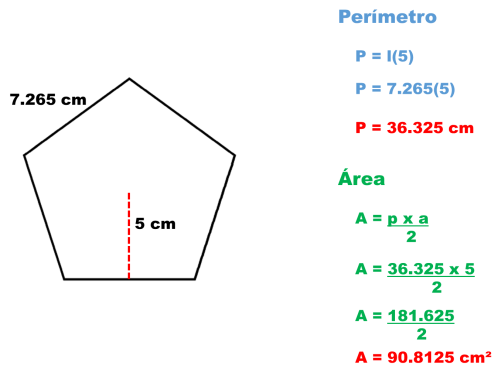
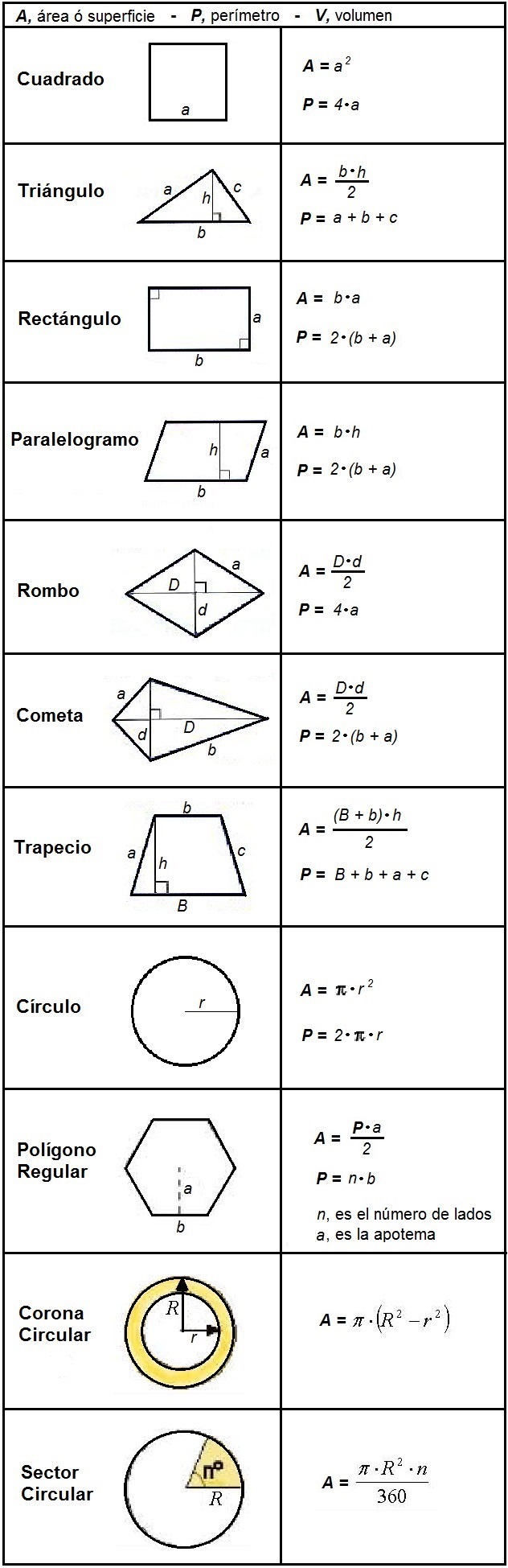
Perímetros y áreas de los polígonos

POLÍGONO REGULAR

Un polígono regular es un polígono con todos los lados y ángulos iguales.

Elementos del polígono regular

Existen varios elementos del polígono regular que los caracterizan.

Centro (C): es el punto del polígono regular que equidista a todos los vértices.
Lado (L): es uno de los n segmentos que delimitan el perímetro del polígono.
Vértice (V): punto de unión de dos lados. Existen tantos vértices como lados tiene el polígono (n).
Radio (r): es el segmento que une el centro con un vértice
Apotema (ap): segmento que une el centro con el punto medio de un lado. Laapotema es perpendicular a dicho lado.
Apotema de un polígono regular

La apotema de un polígono regular puede obtenerse sabiendo el número de lados (N) del polígono y lo que mide cada lado (L).

Sea el ángulo central α el ángulo que forman las dos líneas que unen el centro delpolígono (O) y dos vértices consecutivos. Éste se calcula como:

Mediante la tangente de la mitad del ángulo central y un lado (L), se calcula la apotema (ap) del polígono regular.
Área del polígono regular

El área de un polígono regular se calcula a partir de su perímetro y su apotema. Sea P el polígono regular con Nlados, su área es:

En un polígono regular, el perímetro se puede determinar por el producto del número de lados por la longitud de uno de los lados, es decir, Perímetro=N·L. O sea:

Perímetro del polígono regular

El perímetro de un polígono regular es la suma de todos sus lados. Como todo polígono regular tiene todos sus costados iguales, el perímetro será el producto del número de lados delpolígono (N) por la longitud de uno de ellos (L):